Signed sets and ballots and naturality

This is blog post #3 in a series on signed sets and ballots (the previous posts are here and here).

Naturality, isomorphism, and equipotence

When are two species isomorphic? Since species are, by definition, functors \(\mathbb{B} \to \mathbf{FinSet}\), the obvious answer is “when they are isomorphic as functors”, that is, when there is a natural isomorphism between them.

Let’s unpack definitions a bit. Recall that \(\mathbb{B}\) is the groupoid (i.e. category with all morphisms invertible) of finite sets and bijections, and \(\mathbf{FinSet}\) is the category of finite sets and total functions.

Given two functors \(F, G : \mathbb{B} \to \mathbf{FinSet}\), a natural isomorphism is some family of bijections \(\psi_U : F[U] \leftrightarrow G[U]\) such that for any bijection \(\varphi : U \leftrightarrow V\), the following square commutes:

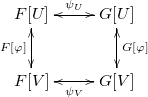
Think of \(\varphi\) as a relabelling—that is, a 1-1 correspondence between labels in \(U\) and labels in \(V\). By functoriality of \(F\) and \(G\), we can lift \(\varphi\) to relabel whole structures, via \(F[\varphi]\) and \(G[\varphi]\). The whole square then says that the family of correspondences \(\psi\) “commute with relabelling”—that is, intuitively, \(\psi\) can’t “look at” the labels at all, because it has to “do the same thing” even when we change the labels out from under it. It operates based solely on the structure present in the \(F\)- or \(G\)-structures—which by functoriality must be independent of the labels—and not based on the identity or structure of the set of labels itself.

All this generalizes readily to virtual species: recall that virtual species consist of pairs of species \((P,N)\), where we define \((P_1, N_1)\) to be equivalent to \((P_2, N_2)\) if and only if \(P_1 + N_2\) is (naturally) isomorphic to \(N_1 + P_2\). That is, isomorphism of virtual species already has natural isomorphism of regular species baked into it by definition.

Now, recall the signed involution from my previous post. Since it depends on a chosen linear order, it is not a natural isomorphism: an arbitrary relabelling certainly need not preserve the ordering on the labels, so the involution is not preserved under relabelling.

This brings up the natural (haha) question: is it possible to give a natural isomorphism between signed sets and signed ballots? If so, we would certainly prefer it to this involution that makes use of a linear order. But sadly, the answer, it turns out, is no. Let \(k\) range from \(0\) to \(n\). We are looking for a natural isomorphism

in the case that \(n\) is odd, or

when \(n\) is even.

Notice that in any case, whether positive or negative, the \(E_n\)-structure will be fixed by any relabelling which is a permutation (because permuting the elements of a set does not change the set). Hence, any natural isomorphism must send it to some structure which is also fixed by all permutations. But the only such ballot structure is the one consisting of a single part containing all the elements. This ballot has an odd number of parts, so there cannot be a natural isomorphism in the case that \(n\) is even—we would have to match the \(E_n\) structure with some even-sized ballot which is fixed by all permutations of the labels, but there are none. Hence there is no natural isomorphism, which by definition would have to work for all \(n\).

But what about for odd \(n\)? Can we have a natural isomorphism between the structures restricted to the case when \(n\) is odd? In fact, no: we can make a more general argument that applies for any \(n > 1\). Consider the \(n!\) different ballots consisting of \(n\) separate singleton parts. Each of these is fixed by no permutations other than the identity. So, under a natural isomorphism they would all have to map to ballots of the opposite parity which are also fixed by no permutations other than the identity: but by the Pigeonhole Principle, any ballot with fewer than \(n\) parts must have at least one part containing more than one element, and will therefore be fixed under any permutation that only touches the elements in that part.

In this situation—when there is a 1-1 correspondence between species, but not a natural one—we say the species are equipotent but not isomorphic. The species have the same number of structures of each size, and hence exactly the same generating function, but they are not (naturally) isomorphic: it is possible to tell them apart by looking at how structures behave under relabelling. Another classic example of this phenomenon is the species of lists and the species of permutations: each has exactly \(n!\) labelled structures of size \(n\), but they are not naturally isomorphic. Lists have no symmetry at all, that is, they are fixed by no permutations other than the identity, but permutations, in general, do have some symmetry. For example, any permutation \(p\) is fixed when the labels are permuted by \(p\) itself: the permutation \((123)\) is the same as the permutation \((231)\). The classic combinatorial proof that there are the same number of lists and permutations also uses an extra linear order on the labels.

Subset parity

A classic lemma in combinatorics states that any nonempty finite set has the same number of even and odd subsets. In fact, I recently wrote a proof of this on my other blog. Since it’s written for a more general audience, it’s spelled out there in quite a lot of detail; but if you understand the idea of signed involutions, the classic combinatorial proof is quite simple to state: given a set \(S\), pick some \(a \in S\), and define a signed involution on subsets of \(S\) (signed according to the parity of their size) by “toggling” the presence of \(a\). That is, given \(X \subseteq S\), if \(a \in X\) then take it out, and if \(a \notin X\) then add it in. This is clearly an involution and sends even subsets to odd and vice versa.

However, this involution is not natural—it depends on the choice of \(a\).¹ Is it possible to prove it via a natural correspondence? In fact, that’s one of the things Anders Claesson’s original post—the one that got me started down this whole rabbit hole—was trying to do. Unfortunately, hidden in the middle of his proof was an assumed correspondence between signed sets and signed ballots, and as we’ve seen, this correspondence actually cannot be proved naturally. (I should reiterate that in no way do I mean to disparage his post—it’s still a great post with a lot of cool insights, not to mention a nice framework for thinking about multiplicative inverses of species. It just doesn’t quite accomplish one of the things he thought it was accomplishing!)

Now, at this point, all we know is that the particular argument used in that post is not, in fact, natural. But that doesn’t necessarily mean a natural correspondence between even and odd subsets is impossible. However, it turns out that it is (mostly) impossible: we can give a more direct argument that, in fact, there is no natural proof—that is, the species of odd subsets and the species of even subsets are equipotent but not naturally isomorphic.

The proof is quite simple, and along similar lines as the proof for signed sets and ballots. Note that the empty subset is fixed by all permutations, as is the maximal subset—and these are clearly the only such subsets. So any natural correspondence must match these subsets with each other—but when \(n\) is even they have the same parity.

What about if we restrict to the case when \(n\) is odd? Unlike the case of signed sets and ballots, it turns out that we actually can give a natural proof in this case! The involution to use is the one that simply sends any \(X \subseteq S\) to its complement \(S - X\). This is clearly an involution, and since \(|S|\) is odd, it reverses the parity as required. It also does not depend at all on the elements of \(S\) or any assumed structure on them, that is, it commutes perfectly well with relabelling.

This corresponds nicely with an observation we can make about Pascal’s triangle: it is easy to see that the alternating sum of any odd row is \(0\), for example, \(1 - 5 + 10 - 10 + 5 - 1 = 0\), since the entries are all duplicated, with one positive and one negative version of each. However, for even rows it is not quite so obvious: why is \(1 - 4 + 6 - 4 + 1 = 0\)? To show this cancels to give 0 we must “split up” some of the numbers so that one part of them cancels with one number and another part cancels with another; that is, we cannot necessarily treat all the subsets of a given size uniformly. But subsets of a given size are completely indistinguishable up to relabelling—hence the necessity of some extra structure to allow us to make the necessary distinctions.