Catsters guide

Introduction

In an attempt to solidify and extend my knowledge of category theory, I have been working my way through the excellent series of category theory lectures posted on Youtube by Eugenia Cheng and Simon Willerton, aka the Catsters.

Edsko de Vries used to have a listing of the videos, but it is no longer available. After wresting a copy from a Google cache, I began working my way through the videos, but soon discovered that Edsko’s list was organized by subject, not topologically sorted. So I started making my own list, and have put it up here in the hopes that it may be useful to others. Suggestions, corrections, improvements, etc. are of course welcome!

As far as possible I have tried to arrange the order so that each video only depends on concepts from earlier ones. Along with each video you can also find my cryptic notes; I make no guarantee that they will be useful to anyone (even me!), but hopefully they will at least give you an idea of what is in each video. (For some of the earlier videos I didn’t take notes, so I have just copied the description from YouTube.)

I have a goal to watch two videos per week (at which rate it will take me about nine months to watch all of them); I will keep this list updated with new video links and notes as I go.

Terminal and Initial objects

Terminal and initial objects 1

http://youtu.be/yeQcmxM2e5I

• Definition and examples of terminal objects
• Sketch of proof that terminal objects are unique up to unique isomorphism

Terminal and initial objects 2

http://youtu.be/9vhWpOVPlIE

• Proof that terminal objects are unique
• Examples of categories without terminal objects

Terminal and initial objects 3

http://youtu.be/yaPwKu5fHqI

• Definition and examples of initial objects

Products and Coproducts

Products and coproducts 1

http://youtu.be/upCSDIO9pjc

• Definition of products
• Example: cartesian product of sets
• \(B \times A\) and \(A \times B\) as two (isomorphic) products
• Uniqueness up to unique isomorphism

Products and coproducts 2

http://youtu.be/BqRkULEhG40

• More on uniqueness up to unique isomorphism
• Examples and non-examples of products

Products and coproducts 3

http://youtu.be/TCQWHOUBwDE

• Definition and example of coproduct

Products and coproducts 4

http://youtu.be/n6nBgszToBE

• Definition of the morphisms \((f,g)\) and \(f \times g\)
• The diagonal
• Products with the terminal object

Pullbacks and Pushouts

Pullbacks and pushouts 1

http://youtu.be/XGysPJvCXOc

• Definition of pullback
• Example: pullbacks in \(\mathbf{Set}\)

Pullbacks and pushouts 2

http://youtu.be/LkkallToFQ0

• Definition of pushouts
• Example: pushouts in \(\mathbf{Set}\)
• Pullback/pushout example of intersection/union of sets

Natural transformations

Natural transformations 1

http://www.youtube.com/watch?v=FZSUwqWjHCU

• Definition of natural transformations.
• Naturality squares.
• Intuition about natural transformations based on homotopy.
• Alternative definition of natural transformation analogous to usual homotopy definition: a natural transformation is a functor \(C \times I \to D\) where \(I\) is the “categorical interval”, i.e. the two-object category with a single nontrivial morphism.

Natural transformations 2

http://youtu.be/XnrqHd39Cl0

• Vertical composition of natural transformations.
• Functor categories.
• Horizontal composition of natural transformations
  • Note there are two ways to define horizontal composition, and they are equal by naturality.

Natural transformations 3

http://youtu.be/EG5xUYXHFeU

• Whiskering (though they don’t call it that yet).
• Horizontal composition as vertical composition of two whiskerings (in two different ways, which are equal by naturality).
• Interchange law: proof by commutativity of whiskering.

Natural transformations 3A

http://youtu.be/fsfzEz6qAGQ

• Define terminology “whiskering”.
• Note vertical composition of “right-whiskered fish” works because of functoriality (of functor we whiskered by).
• Vertical composition of “left-whiskered fish” comes by definition of vectical composition for natural transformations.
• So in the end, interchange depends on three things: definition of vertical composition; functoriality; naturality.

Representable functors and the Yoneda Lemma

Representables and Yoneda 1

http://youtu.be/4QgjKUzyrhM

• Definition of representable functors (co- or contravariant): those which are naturally isomorphic to \(H^A\) or \(H_A\) for some \(A\).
  • Contravariant: \(H_A : C^{\text{op}} \to \mathbf{Set}\); \(H_A(X) = C(X,A)\).
  • Covariant: \(H^A : C \to \mathbf{Set}\); \(H^A(X) = C(A,X)\).
• Is there a functor \(A \to H_A\)? Yes, the Yoneda embedding \(Y\):
  • \(Y(A) = H_A\)
  • \(Y(f) = H_f\), where \(H_f : H_A \to H_B\) is postcomposition with \(f\). \(H_f\) is a natural transformation; its component at \(X\) has type \(H_f(X) : H_A(X) \to H_B(X) = C(X,A) \to C(X,B)\). Postcomposing an arrow in \(C(X,A)\) with \(f : A \to B\) yields an arrow in \(C(X,B)\).

Representables and Yoneda 2

http://youtu.be/eaJmUUogb6g

• Proof that Yoneda embedding \(C \to [C^{\text{op}}, \mathbf{Set}]\) sends morphisms \(f\) to natural transformations \(H_f\). Comes down to the fact that composition in the category is associative.

Representables and Yoneda 3

http://youtu.be/TLMxHB19khE

• Look at natural transformations from \(H_A\) to some other (contravariant) functor \(F\). Big idea: such natural transformations \(\alpha\) are entirely determined by where \(\alpha_A\) sends \(1_A\).
• Yoneda lemma: \(F\ A \cong [C^{\text{op}}, \mathbf{Set}](H_A, F)\) (natural in \(A\) and \(F\)). I.e. the set of objects in \(F\ A\) is isomorphic to the hom-set of natural transformations between \(H_A\) and \(F\).

Adjunctions (part 1)

Adjunctions 1

http://youtu.be/loOJxIOmShE

• Given categories \(C\) and \(D\) and functors \(F : C \to D\) and \(G : D \to C\), we have the following situations:
  • Isomorphism: \(1 = GF\), \(FG = 1\)
  • Equivalence: \(1 \cong GF\), \(FG \cong 1\)
  • Adjunction: \(\eta : 1 \Rightarrow GF\), \(\varepsilon : FG \Rightarrow 1\) So we can think of an adjunction as a “weaker sort of equivalence”.
• \(\eta\) and \(\varepsilon\) are subject to triangle identities: \(F \stackrel{F\eta}{\Longrightarrow} FGF \stackrel{\varepsilon F}{\Longrightarrow} F\) is the identity, and similarly for \(\eta G ; G \varepsilon\).
• These laws can be expressed as commuting diagrams of 2-cells: draw \(\eta\) and \(\varepsilon\) as 2-cells and paste them in two different ways.

Adjunctions 2

http://youtu.be/JEJim3t-N9A

• Alternate definition of adjunction \(F \dashv G\): an isomorphism \(D(F X, Y) \cong C(X, G Y)\) natural in \(X\) and \(Y\).
• What “natural in \(X\) and \(Y\)” means here.
• Hint: sending identity morphisms across the iso gives us \(\eta\) and \(\varepsilon\) from the first definition. Proof deferred to Adjunctions 4.

Adjunctions 4

http://youtu.be/nP5XQ6OBHHY

• Note: Adjunctions 4, not 3, follows on to 2.
• Given: an isomorphism \(D(FX,Y) \cong C(X,GY)\) which is natural in \(X\) and \(Y\).
• Notation: write application of the isomorphism as an overbar.
• Construct the two squares implied by naturality. Follow them each around in both directions (since they involve a natural isomorphism) to get four equations in total governing how the iso interacts.
• Define \(\eta\) and \(\varepsilon\) by applying the isomorphism to appropriate identity morphisms. Naturality and the triangle identities follow from the above four equations.

Monads

Monads 1

http://youtu.be/9fohXBj2UEI

• Monads give us a way to talk about algebraic theories (monoids, categories, groups, etc.).
• Definition of a monad:
  • Functor \(T : C \to C\)
  • “unit” \(\eta : 1 \Rightarrow T\)
  • “multiplication” \(\mu : T^2 \Rightarrow T\)
  • with unit and associativity laws.
• Note what is meant by a commutative diagram of natural transformations
• Example: monad for monoids (aka the list monad)
  • \(C = \mathbf{Set}\)
  • \(T = X \mapsto X^*\), maps a set \(X\) to set of words in \(X\) (i.e. lists)
  • \(\eta\) is singleton
  • \(\mu\) is concatenation
  • Note, unit and associativity for monad is different than unit and associativity of monoids, which has already been encoded in the definition of \(T\).

Monads 2

http://youtu.be/Si6_oG7ZdK4

• Proof that the list monad (“monad for monoids”) is in fact a monad
• Example: monad for small categories
  • \(C = \mathbf{Gph}\), category of graphs
  • \(T\) makes the free category on a graph (morphisms = paths in the underlying graph)
  • With only one object, this reduces to the monad for monoids.
  • Proof of monads laws is basically the same as for the list monad.

Monads 3

http://youtu.be/eBQnysX7oLI

• Algebras for monads. Monads are supposed to be like algebraic theories; algebras are models.
• An algebra for a monad \((T : C \to C, \eta, \mu)\) is an object \(A \in C\) (the “underlying object”) equipped with an “action” \(\theta : T\ A \to A\), satisfying the “obvious” axioms (\(\theta\) must interact “sensibly” with \(\eta\) and \(\mu\)).
  • \(\eta ; \theta = 1\)
  • \(\mu ; \theta = T \theta ; \theta\)
• Example: \(C = \mathbf{Set}\), \(T\) = list monad (“monad for monoids”)
  • An algebra is a set \(A\) equipped with \(\theta : [A] \to A\)
  • First axiom says \(\theta\) must simply project element out of length-one list.
  • Other axiom is essentially associativity.
  • That is, algebras for the list monad are monoids.
• Example for monad of categories (from last time) works the same way.

Monads 3A

http://youtu.be/uYY5c1kkoIo

More on monoids as monad algebras of the list monad.

• Given a monad algebra \(\theta : [A] \to A\), construct the monoid:
  • whose underlying set is \(A\)
  • \(a \cdot b = \theta [a,b]\)
  • \(\varepsilon = \theta []\).
• The monad algebra law for \(\eta\) (a triangle) just says that \(\theta\) can’t do anything interesting on one-element lists: it has to just return the single element.
• Identity and associativity laws for the monoid come from the other monad algebra law, saying how \(\theta\) interacts with \(\mu\) (a square), and from how the list functor is defined. We start with a way of mapping lists down to values, which bakes in the idea that it doesn’t matter how we associate the list.

Monads 4

http://youtu.be/Cm-O_ZWEIGY

Monad algebras form a category (called \(\mathbf{Alg}\ T\)).

• Given two monad algebras \(\theta : T A \to A\) and \(\varphi : T B \to B\), a morphism between them consists of a morphism of underlying objects, \(f : A \to B\), such that the obvious square commutes.

• Example. List monad again. \(C = \mathbf{Set}, T = []\). A morphism of monoids is a function \(f : A \to B\) such that \(f (xy) = f(x)f(y)\). See how this equation arises from the commuting square for monad morphisms, by starting with a 2-element list in upper left and following it around.

• Given a particular mathematical theory, can it be expressed as the category of algebras for some monad? I.e. given a category \(D\), is it equivalent to \(\mathbf{Alg}\ T\) for some \(T\)? (Answer: no, not in general, e.g. category of topological spaces can’t.)

• But this is still an interesting question, more or less the question of “monadicity”. Category \(D\) said to be monadic over category \(C\) if \(D\) can be expressed as category of algebras of monads over \(C\).

Adjunctions and monads

Adjunctions 3

http://youtu.be/2i_PpYsl8b8

• Note: depends on monads.
• Examples of adjunctions:
  • between the category of sets and the category of monoids: \(\text{Free} \dashv \text{Forget}\)
  • similarly between category of graphs and category \(\mathbf{Cat}\) of (small) categories.

  In general, free functors are left adjoint to forgetful functors. (How to remember the direction: “left” has four letters, just like “free”.)

• Every adjunction \((F \dashv G : C \to D, \eta, \varepsilon)\) gives rise to a monad \((GF, \eta, \mu = G \varepsilon F)\). Check monad laws:
  • Monad triangle laws are just adjunction triangle laws with extra \(G\) or \(F\) everywhere.
  • Monad associativity law is naturalty for \(\varepsilon\), or something like that.

Adjunctions 5

http://youtu.be/xqLgGB7Hv7g

“Every monad comes from an adjunction via its category of algebras.”

Last time we showed every adjunction gives rise to a monad. What about the converse?

Answer: yes. In fact, given a monad, there is an entire category of adjunctions which give rise to it, which always has initial and terminal objects: these are the constructions found by Kleisli and by Eilenberg-Moore, respectively. Intuitively, any other adjunction giving rise to the monad can be described by the morphisms between it and the Kleisli and Eilenberg-Moore constructions.

Let \((T : C \to C, \eta, \mu)\) be a monad.

• Terminal solution (Eilenberg-Moore): consider category \(\mathbf{Alg}\ T\) of \(T\)-algebras, also written \(C^T\). We construct an adjunction \(F \dashv G : C \to C^T\). (Intuition: \(F : C \to C^T\) “freely” constructs a \(T\)-algebra; \(G : C^T \to C\) “forgets” the algebra structure.)

  • \(G : C^T \to C\) is easy to construct: \((A, \theta : T A \to A) \mapsto A\).

  • What about \(F : C \to C^T\)? Sends \(A\) to the “free” \(T\)-algebra on \(A\), with underlying set \(T A\). Then evaluation map is \(\mu\). That is, \(F A = (T A, \mu : T (T A) \to T A)\). Need to check that this definition of \(F\) really gives a monad algebra as a result. In this case the monad algebra laws are just the monad laws for \(T\)!

  • Now define a unit and counit. \(\eta_A : A \to GFA = A \to TA\) is just the \(\eta\) for the monad. \(\varepsilon_\theta : FG(A,\theta) \to (A,\theta)\) is an algebra morphism from the free algebra on \(A\) (i.e. \((TA, \mu)\)) to \((A,\theta)\): in fact, \(\theta\) itself is such a morphism, by the second algebra law.

  • Prove triangle laws for \(\eta\) and \(\varepsilon\): exercise for the watcher/reader.

Adjunctions 6

http://youtu.be/Ht1mQ97Zq2k

This time, initial solution to “does a monad give rise to any adjunctions”: Kleisli.

• The Kleisli category for a monad \(T\) on category \(C\), written \(\mathbf{Kl}(T)\) or \(C_T\)
  • Objects: objects of \(C\).
  • Morphisms: \(C_T(A,B) :\equiv C(A,T B)\).
  • Composition: given \(f : A \to T B\) and \(g : B \to T C\), produce \(f ; T g ; \mu : A \to T C\).
  • Identity: \(\eta : A \to T A\).
  • Category axioms come from monad axioms. Associativity comes from associativity and naturality of \(\mu\); unit laws come from unit laws for \(\eta\).

• Intuition: this is the category of free algebras: \(A \to T B = GFB\) is equivalent, under the adjunction, to \(F A \to F B\), morphism between free algebras.

• Note, for the Eilenberg-Moore category (last time) it was complicated to define the objects and simple to define the morphisms. For Kleisli, it’s the other way around. “Conservation of complicatedness.”

Adjunctions 7

http://youtu.be/D8g9xnVr0Lg

The adjunction that comes from the Kleisli category, giving rise to the original monad \(T\).

Again, let \((T : C \to C, \eta, \mu)\) be a monad. We will construct \(F_T \dashv G_T : C \to C_T\), where \(C_T\) is the Kleisli category defined in Adjunctions 6, with \(G_T F_T = T\).

• \(F_T : C \to C_T\) sends objects to “free algebras”
  • Identity on objects.
  • On morphisms, sends \(f : A \to B\) to \(\eta ; T f : A \to T B\) (equivalently \(f ; \eta\)).
• \(G_T : C_T \to C\) sends a “free algebra” to its “underlying object”
  • Sends \(A\) to \(T A\).
  • Sends \(f : A \to T B\) to \(T f ; \mu : T A \to T B\).
• Unit and counit
  • \(\eta : A \to G_T F_T A = T A\) we can take as the \(\eta\) of the monad.
  • \(\varepsilon : F_T G_T A = T A \to T A\) we can take to be id.
• Adjunction laws come down to monad laws (left to viewer).

Given a monad \(T\) on \(C\), we have a category of adjunctions \(\mathbf{Adj}(T)\) giving rise to \(T\) (morphisms are functors making everything commute). \(C_T\) is the initial object and \(C^T\) is terminal.

Question of monadicity: given an adjunction \(F \dashv G\), is \(D \cong C^T\)? If so, say “\(D\) is monadic over \(C\)”, i.e. everything in \(D\) can be expressed as monad algebras of \(C\). Or can say the adjunction is a “monadic adjunction”. Can also say that the right adjoint (forgetful functor \(G\)) “is monadic”. Monadic adjunctions are particularly nice/canonical.

String diagrams

String diagrams 1

http://youtu.be/USYRDDZ9yEc

Way of notating natural transformations and functors. Poincare dual: 0D things (points, i.e. categories) become 2D (regions), 1D things (lines, i.e. functors) stay 1D, 2D things (cells, i.e. natural transformations) become 0D.

String diagrams should be read right-left and bottom-top.

Horizontal and vertical composition of NTs correspond to horizontal and vertical juxtaposition of string diagrams.

Can leave out vertical lines corresponding to identity functor.

String diagrams 2

http://youtu.be/JeGhNhgOTuk

Recall the interchange law, which says that vertical and horizontal composition of natural transformations commute. This guarantees that string diagrams are well-defined, since the diagram doesn’t specify which happens first.

Whiskering is represented in string diagrams by horizontally adjoining a straight vertical line.

String diagrams 3

http://youtu.be/pmvVE8AGAEA

Given an adjunction \(F \dashv G\), we have natural transformations \(\varepsilon : FG \to 1\) and \(\eta : 1 \to GF\), and two laws given by triangles. What do these look like as string diagrams? \(\varepsilon\) is a cap, \(\eta\) a cup, and the triangle laws look like pulling wiggly strings straight!

String diagrams 4

http://youtu.be/YNC5faXshAk

Monads in string diagrams. Draw \(\mu\), \(\eta\), and the monad laws as nice-looking string diagrams with nice topological intuition.

String diagrams 5

http://youtu.be/kiXjcqxVogE

Seeing how monads arise from adjunctions, using string diagrams.

Pipe cleaners

These are presented without any commentary or explanation that I can find. Each of the below videos just presents a 3D structure made out of pipe cleaners with no explanation. Maybe there is some other catsters video that presents a motivation or explanation for these; if I find it I will update the notes here. I can see that it might have something to do with string diagrams, and that you can make categories out of these sorts of topological structures (e.g. with gluing as composition) but otherwise I have no clue what this is about.

• Open-closed cobordisms 1: http://youtu.be/Jb1ZHLXBMy4
• Open-closed cobordisms 2 (“zig-zag-ator”): http://youtu.be/zQMhXy1-YNM
• Open-closed cobordisms 3 (“cut-off pair of pants”): http://youtu.be/_raQJYpEnU8

There is also:

• Klein bottle: https://www.youtube.com/watch?v=kteH2ZBW9Lg

This is a nice 5-minute presentation about Klein bottles, complete with pipe cleaner model. Though it seems to have little to do with category theory.

Also also:

• Outtakes: https://www.youtube.com/watch?v=guVjFOfi2o0

This has nothing to do with either pipe cleaners or category theory, but it is midly amusing.

General Limits and Colimits

General limits and colimits 1

http://www.youtube.com/watch?v=g47V6qxKQNU

Defining limits in general, informally.

• The thing we take a limit of is called a diagram (a collection of objects and morphisms). A limit of a diagram is a universal cone.
• A cone over a diagram is an object (vertex) together with morphisms (projection maps) to all objects in the diagram, such that all triangles commute.
• Universal cone is the “best” one, through which all other cones factor, i.e. there is a unique morphism from the vertex of one to the other such that all the relevant triangles commute.

General limits and colimits 2

http://www.youtube.com/watch?v=SpCyaNi257w

Examples of limits.

• Terminal objects: limit over the empty diagram.
• Products: limit over discrete diagram on two objects.
• Pullback: limit over a “cospan”, i.e. a diagram like \(X \to Y \leftarrow Z\). Note that we usually ignore the edge of the cone to \(Y\), since it is uniquely determined by the edges to \(X\) and \(Z\).
• Equalizer: limit over a parallel pair of arrows.

General limits and colimits 3

http://www.youtube.com/watch?v=U3nzEUEnLKQ

• Note: requires natural transformations.
• Formal definitions of:
  • Diagram (functor from an index category)
  • Cone (natural transformation from constant functor to diagram).

General limits and colimits 4

http://youtu.be/7B4cawdLAPg

• Requires Yoneda.

• Formal definition of a limit: given a diagram \(D : I \to C\), a limit for \(D\) is an object \(U\) together with a family of isomorphisms \(C(V,U) \cong [I,C](\Delta_V, D)\) natural in \(V\). I.e. a natural correspondence between morphisms \(V \to U\) (the “factorization” from one cone to another) and morphisms (i.e. natural transformations) from \(\Delta_V\) to \(D\) in the functor category \([I,C]\) (i.e. cones over \(D\) with vertex \(V\)). That is, every cone with vertex \(V\) has a unique factorization morphism, and vice versa!. The “vice versa” part is the surprising bit. If we have a limit then every morphism is the factorization for some cone to the universal cone.

• If we set \(V = U\) then \(C(U,U) \cong \dots\) etc. In particular \(1_U : C(U,U)\) corresponds to some cone, which is THE universal cone. The Yoneda lemma says (?) that the entire natural isomorphism is determined by this one piece of data (where \(1_U\) goes). Note that both \(C(-,U)\) and \([I,C](\Delta_-, D)\) are functors \(C^{\text{op}} \to \mathbf{Set}\). The Yoneda lemma says that a natural transformation from \(C(-,U) = H_U\) to \([I,C](\Delta_-, D)\) is isomorphic to \([I,C](\Delta_U, D)\) — i.e. a cone with vertex \(U\), the universal cone.

• The universality of this cone apparently comes from naturality.

General limits and colimits 5

http://youtu.be/Ud_k4HFIogQ

• Requires adjunctions.
• Notation for limits. Categories that “have all limits (of a given shape)”.
• The natural isomorphism defining a limit can be seen as an adjunction \(\Delta \dashv \lim_{I \leftarrow}\) where \(\Delta : C \to [I,C]\), and \(\lim_{I \leftarrow} : [I,C] \to C\) is the functor that takes a diagram and produces its limit.
• Claim: this is an adjunction if \(C\) has all \(I\)-limits. Need to show that the iso is also natural in \(D\), and that \(\lim_{I \leftarrow}\) is actually a functor.

General limits and colimits 6

http://youtu.be/9UOdrRF_pNc

Colimits using the same general formulation. “Just dualize everything”.

• Cocone (“cone under the diagram”) is an object with morphisms from the objects in the diagram such that everything commutes.

• Universal cocone: for any other cocone, there is a unique morphism from the universal cocone to the other cone which makes everything commute. Note it has to go that direction since the universal cocone is supposed to be a “factor” of other cocones.

• In Eugenia’s opinion the word “cocone” is stupid.

• More generally: natural isomorphism between cocones and morphisms. \(C(\lim_{\to I}, V) \cong [I,C](D, \Delta_V)\). Limits in \(C\) are the same as colimits in \(C^{op}\), and vice versa.

• All limits are terminal objects in a category of cones (and colimits are initial objects).

• Since terminal objects are initial objects in \(C^{op}\) (and vice versa), we can even say that all universal properties are initial objects (and terminal objects) somewhere.

Slice and comma categories

Slice and comma categories 1

https://www.youtube.com/watch?v=f4jpvwwnq_s

Slice category. Given a category \(C\), fix an object \(X \in C\). Then we define the slice category \(C/X\) by

• Objects are pairs \((A,p)\) where \(p : A \to X\).
• Morphisms from \((A,p)\) to \((B,q)\) are morphisms \(h : A \to B\) in \(C\) which make the triangle commute.

Coslice category, or “slice under” category \(X/C\) is the dual of \(C/X\), i.e. objects are pairs \((A,p)\) where \(p : X \to A\), etc.

• If \(C\) has a terminal object \(1\), \(C/1 \cong C\). (Dually, \(0/C \cong C\).)

• Products in \(C/X\) are pullbacks in \(C\) having \(X\) as a corner. (Dually, coproucts in \(X/C\) are pushouts.)

Slice and comma categories 2

http://youtu.be/W6sG5uraex0

Comma categories are a generalization of slice categories. Fix a functor \(F : C \to D\) and an object \(X \in D\). Then we can form the comma category \(F \downarrow X\).

• Objects: pairs \((c \in C, p : F c \to X)\). Image of some object under \(F\) and an arrow from it to \(X\).
• Morphisms are morphisms \(f\) in \(C\) such that \(F f\) makes the relevant diagram commute.

Of course we can dualize, \(X \downarrow F\) (“cocomma” sounds even stupider than “cocone”, perhaps).

Apparently comma categories give us nice ways to talk about adjunctions.

Let’s generalize even more! Fix the functor \(F\) but not the object \(X \in D\). Then we can form \(F \downarrow D\):

• Objects: triple \((c \in C, X \in D, p : F C \to X)\).
• Morphism \((c, X, p) \to (c', X', p')\) is a pair of morphisms \(c \to c'\) and \(X \to X'\) such that the relevant square commutes.

Can also dualize, \(D \downarrow F\).

An even further generalization! Start with two functors \(F : C \to D\), \(G : E \to D\). Form \(F \downarrow G\):

• Objects: triples \((c \in C, e \in E, p : F c \to G e)\).
• Morphisms: obvious generalization.

In fact, all of these constructions are universal and can be seen as limits/colimits from the right point of view. “Next time”. (?)

Coequalisers

Coequalisers 1

https://youtu.be/vYktRTtulek

Coequalisers are a colimit. Show up all over the place. Give us quotients and equivalence relations. Also tell us about monadicity (given an adjunction, is it a monadic one?).

Definition: a coequaliser is a colimit of a diagram consisting of two parallel arrows.

More specifically, given \(f,g : A \to B\), a coequaliser is an object \(C\) equipped with \(e : B \to C\) such that \(f;e = g;e\), with a universal property: given any other \(s : B \to V\) with \(f;s = g;s\), \(s\) factors uniquely through \(e\).

• Example: in \(\mathbf{Set}\): coequaliser of \(f,g : A \to B\) is a quotient \(B/\sim\), where \(\sim\) is the equivalence relation generated by \(f(a) \sim g(a)\) for all \(a \in A\).

• Conversely, we can start with an equivalence relation and build it using a coequaliser. Given: an equivalence relation \(R \subseteq B \times B\). Note we have \(\pi_1, \pi_2 : R \to B\). Coequaliser is equivalence classes of \(R\).

Coequalisers 2

https://www.youtube.com/watch?v=DMSPS6us__Y

Quotient groups as coequalisers. Consider a group \(G\) and a normal subgroup \(H \triangleleft G\). In the category of groups, consider two parallel maps \(H \to G\): the inclusion map \(\iota\), and the zero map \(0\) which sends everything to the identity element \(e \in G\). Claim: the coequaliser of these two maps is the quotient group \(G/H\), together with the quotient map \(G \to G/H\).

Let’s see why. Suppose we have another group \(V\) with a group homomorphism \(\theta : G \to V\) such that \(\iota ; \theta = 0 ; \theta = 0\); that is, \(\theta(h) = e\) for all \(h \in H\). We must show there is a unique homomorphism \(G/H \to V\) which makes the diagram commute.

Notation: \(g \in G\) under the quotient map gets sent to \([g] = gH\) (\(g_1 \sim g_2\) iff \(g_2 g_1^{-1} \in H\)). For the homomorphism \(G/H \to V\), send \([g]\) to \(\theta(g)\). Note this is required to make things commute, which gives us uniqueness; we must check this is well-defined and a group homomorphism. If \(g_1 \sim g_2\) then \(g_2 g_1^{-1} \in H\). By definition, \(\theta(g_2 g_1^{-1}) = e\), and since \(\theta\) is a group homomorphism, \(\theta(g_2) = \theta(g_1)\). Hence it is well-defined, and must additionally be a group homomorphism since \([g_1] [g_2] = [g_1 g_2]\) and \(\theta\) is a group homomorphism.

Monoid objects

Monoid objects 1

https://www.youtube.com/watch?v=PH-OhkrXXvA

Idea: take the definition of monoids from \(\mathbf{Set}\), and “plunk it” into any other category with enough structure.

• A monoid is:
  • A set \(A\)
  • A binary operation \(a \cdot b\) on \(A\)
  • A unit \(e \in A\)
  • Associativity: \(\forall a,b,c \in A, (ab)c = a(bc)\)
  • Identity: \(\forall a, ea = a = ae\)

Now let’s reexpress this categorically in \(\mathbf{Set}\). Note we have been talking about elements of sets; we have to replace this with use of only objects and morphisms of \(\mathbf{Set}\).

• A monoid (take 2) is:
  • An object \(A \in \mathbf{Set}\)
  • A morphism \(\mu : A \times A \to A\) (note we use Cartesian product structure of \(\mathbf{Set}\))
  • A morphism \(\eta : 1 \to A\)
  • A commutative diagram

  

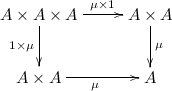
  • A commutative diagram

  

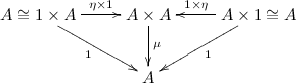
Now we take the definition and port it to any monoidal category.

• A monoid object in a monoidal category \(C\) is:
  • An object \(A \in C\)
  • A morphism \(\mu : A \otimes A \to A\)
  • A morphism \(\eta : 1 \to A\)
  • A commutative diagram

  

  • A commutative diagram

  

Monoid objects 2

https://www.youtube.com/watch?v=7Sf3Y4sesZE

Today: monoid object in the category of monoids is a commutative monoid.

Note first the category of monoids is itself monoidal under Cartesian product. That is, given two monoids \(M\) and \(N\), \(M \times N\) is also a monoid.

Now, what is a monoid object in \(\mathbf{Mon}\)?

• An object \(M \in \mathbf{Mon}\), i.e. a monoid
• Monoid morphisms \(\eta : 1 \to M\) and \(\mu : M \times M \to M\)
• …satisfying unit and associativity laws.

\(\eta : 1 \to M\) is a monoid morphism so it has to send the single object of \(1\) to the unit of \(M\). Hence \(\eta\) is entirely constrained and uninteresting.

\(\mu : M \times M \to M\) has to be a monoid map. That is, \(\mu((a,b) \circ (c,d)) = \mu(a,b) \circ \mu(c,d)\), i.e. \(\mu(a \circ c, b \circ d) = \mu(a,b) \circ \mu(c,d)\). So \(\mu\) has to “commute” with \(\circ\). This is precisely the condition needed to apply Eckmann-Hilton.

Monoid object is also required to satisfy unital and associativity laws, but we can already deduce those from Eckmann-Hilton.

2-categories

2-categories 1

https://www.youtube.com/watch?v=k-RehY4tLdI

Generalization of categories: not just objects and morphisms, but also (2-)morphisms between the (1-)morphisms. Primordial example: categories, functors, and natural transformations.

Note: today, strict 2-categories, i.e. everything will hold on the nose rather than up to isomorphism. A bit immoral of us. [If we let things be a bit looser we get bicategories?]

Recall: a (small) category \(C\) is given by

• A set \(\mathrm{Ob}\ C\) of objects
• for all \(x,y \in \mathrm{Ob}\ C\), a set \(C(x,y)\) of morphisms

equipped with

• identities: for all \(x \in C\) a function \(1 \to C(x,x)\)
• composition: for all \(x,y,z \in C\), a composition function \(C(y,z) \times C(x,y) \to C(x,z)\).
• unit and associativity laws.

To make this into a 2-category, we take the set of morphisms and categorify it. That turns some of the above functions into functors. Thus, a \(2\)-category \(C\) is given by a set of objects along with

• a category \(C(x,y)\) for each \(x,y \in C\)
• a functor \(1 \to C(x,x)\) for each \(x \in C\)
• a composition functor \(C(y,z) \times C(x,y) \to C(x,z)\).
• etc.

(Note: why not turn the set of objects into a category? That’s a good question. Turns out we would get something different.)

Let’s unravel this a bit. If \(C(x,y)\) is a category then the objects are morphisms (of \(C\)) \(x \to y\), and there can also be morphisms (of \(C(x,y)\)) between these morphisms: \(2\)-cells. \(2\)-cells can be composed (“vertical” composition).

We also have the composition functor \(C(y,z) \times C(x,y) \to C(x,z)\). On “objects” (which are \(1\)-cells in \(C\)) the action of this functor is just the usual composition of \(1\)-cells. On morphisms (i.e. \(2\)-cells), it gives us “horiztonal” composition.

Next time: how functoriality gives us the interchange law.

2-categories 2

http://youtu.be/DRGh-HESyag

Interchange in a 2-category comes from functoriality of the composition functor. The key is to remain calm.

The functor is \(C(y,z) \times C(x,y) \to C(x,z)\). On morphisms, it sends pairs of \(2\)-cells to a single \(2\)-cell, the horizontal composite. What does functoriality mean? It means if we have two (vertically!) composable pairs of \(2\)-cells; the functor on their composition (i.e doing vertical composition pointwise) is the same as applying the functor to each (i.e. first doing the horizontal compositions) and then composing (vertically).

Eckmann-Hilton

Eckmann-Hilton 1

https://www.youtube.com/watch?v=Rjdo-RWQVIY

NOTE: There seems to be no catsters video actually explaining what a “bicategory” is. According to the nlab it is a weaker version of a 2-category, where certain things are required to hold only up to coherent isomorphism rather than on the nose.

Eckmann-Hilton argument. Originally used to show all higher homotopy groups are Abelian. We can use it for other things, e.g.

• A bicategory with only one 0-cell and one 1-cell is a commutative monoid.
• A monoid object in the monoidal category of monoids is a commutative monoid. (waaaat)

Idea: given a set with two unital binary operations, they are exactly the same, and commutative — as long as the operations interact in a certain coherent way.

Given a set with two binary operations \(\circ\) and \(\star\), such that

• \(\circ\) and \(\star\) are unital, with the same unit;
• one of them distributes over the other, i.e. \((a \star b) \circ (c \star d) = (a \circ c) \star (b \circ d)\),

then \(\circ = \star\), and the operation is commutative.

Geometric intuition: \(\circ\) and \(\star\) could be vertical and horizontal composition of \(2\)-cells in a bicategory. Then distributivity is just the interchange law.

Proof: use the “Eckmann-Hilton clock”. See video for pictures. Given e.g. \(a \circ b\), “rotate” \(a\) and \(b\) around each other by inserting units and using interchange law.

In fact, it is not necessary to require that the two units are the same: it is implied by the interchange law. Left as an exercise.

Eckmann-Hilton 2

https://www.youtube.com/watch?v=wnRqo7UHa-k

This time, show the interchange law implies the units are the same and associativity.

Let \(v\) be the vertical unit and \(h\) the horizontal unit. Then \(((v \circ h) \star (h \circ v)) = h \star h = h\) but also by interchange law it is equal to \(((v \star h) \circ (h \star v)) = v \circ v = v\), hence \(h = v\).

\((a \circ 1) \star (b \circ c) = a \star (b \circ c)\); interchange gives \((a \star b) \circ (1 \star c) = (a \star b) \circ c\). Since the two operations have to be the same, this gives associativity.

Example. A (small) \(2\)-category with only one \(0\)-cell and only one \(1\)-cell is in fact a commutative monoid. Underlying set is set of \(2\)-cells. Operation is either \(\circ\) or \(\star\), which by Eckmann-Hilton are the same and commutative.

Bicategory case is a bit more complicated, since horizontal composition is not strictly unital. A bicategory with only one \(0\)-cell is a monoidal category. A bicategory with only one \(1\)-cell is a commutative monoid.

Distributive laws

Distributive laws 1

https://www.youtube.com/watch?v=mw4IhOLhDwY

Monads represent algebraic structure; a distributive law says when two algebraic structures interact with each other in a coherent way. Motivating example: multiplication and addition in a ring.

Let \(S\), \(T\) be monads on a category \(C\). A distributive law of \(S\) over \(T\) is a natural transformation \(\lambda : ST \to TS\), satisfying the “obvious” axioms: \(\lambda\) needs to interact properly with the monad structure of \(S\) and \(T\), that is:

• \(\eta_S T ; \lambda = T \eta_S\)

• \(S \lambda ; \lambda S ; T \mu_S = \mu_S T ; \lambda\)

• \(S \eta_T ; \lambda = \eta_T S\)

• \(\lambda T ; T \lambda ; \mu_T S = S \mu_T ; \lambda\)

Example: \(C = \mathbf{Set}\). \(S\) = free commutative monoid monad (“multiplication”), \(T\) = free abelian group monad (“addition”). Define \(\lambda_X : STX \to TSX\): \(TX\) is formal sums of elements of \(X\), like \((a + b + c)\); \(S\) constructs formal products. So we have to send things like \((a + b)(c + d)\) to formal sums of formal products, \(ac + bc + ad + bd\).

In fact we have constructed the free ring monad, \(TS\).

If we start with a monoid and consider the free group on its underlying elements, we can define a product using distributivity; so the free group on a monoid is a group. Formally, the free group monad lifts to the category of monoids (?).

Distributive laws 2

https://www.youtube.com/watch?v=TLgjH9Y8HOc

More abstract story behind our favorite example: combining a group and a monoid to get a ring.

Note: distributive law (at least in this example) is definitely non-invertible: you can turn a product of sums into a sum of products, but you can’t necessarily go in the other direction.

Main result: A distributive law \(\lambda : ST \to TS\) is equivalent to a lift of \(T\) to a monad \(T'\) on \(S\)-\(\mathbf{Alg}\). \(TS\) becomes a monad, and \(TS\)-\(\mathbf{Alg}\) is equivalent to \(T'\)-\(\mathbf{Alg}\).

When is \(TS\) a monad? We need \(\mu : TSTS \to TS\); can do this if we have \(\lambda : ST \to TS\), then use \(\mu_T \mu_S\). The laws for a distributive law ensure that this satisfies the monad laws.

Distributive law is equivalent to a lift of \(T\) to a monad on \(S\)-\(\mathbf{Alg}\)?

• An \(S\)-algebra looks like \(\theta : SX \to X\); we want \(T'\) to send this to another \(S\)-algebra, with carrier \(TX\), i.e. some \(\phi : STX \to TX\). But we have \(T \theta : TSX \to TX\); precomposing with \(\lambda\) gives us what we want, and the distributive law axioms ensure that \(T'\) is a monad on \(S\)-\(\mathbf{Alg}\).

\(TS\)-\(\mathbf{Alg}\) is equivalent to \(T'\)-\(\mathbf{Alg}\)?

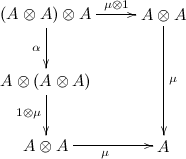
• Since \(T'\) is a monad on \(\mathbf{Alg} S\), a \(T'\)-algebra has an \(S\)-algebra as its underlying object. So given some \(S\)-algebra \(\theta : SX \to X\), a \(T\)’-algebra on it is a morphism of \(S\)-algebras from \(T'\theta\) to \(\theta\), that is,

  

  This essentially says that an algebra for \(T'\) is simultaneously an algebra for \(S\) and an algebra for \(T\) which interact properly via the distributivity law.

• An algebra for \(TS\) is \(\psi : TSX \to X\). Clear that from a \(T'\)-algebra we get a \(TS\) algebra. What about vice versa? Just precompose \(\psi\) with \(\eta_T\) to get an \(S\)-algebra, and with \(T \eta_S\) to get a \(T\)-algebra. A \(TS\)-algebra says how to evaluate e.g. multiplication and additions all mixed up; precomposing with \(\eta\) picks out the stuff with just multiplication or just addition. Apparently one can prove that the algebras you get this way do indeed interact nicely.

Distributive laws 3 (aka Monads 6)

https://www.youtube.com/watch?v=g-SCYArh5RY

Recall that a monad is a functor together with some natural transformations; we can see this as a construction in the \(2\)-category of categories, functors, and natural transformations. We can carry out the same construction in any \(2\)-category \(C\), giving monads in \(C\).

Let \(C\) be a \(2\)-category (e.g. \(\mathbf{Cat}\)). A monad in \(C\) is given by

• a \(0\)-cell \(X\)
• a \(1\)-cell \(T : X \to X\)
• a pair of \(2\)-cells \(\eta : 1 \to T\) and \(\mu : T^2 \to T\)

satisfying the usual monad axioms.

In fact, we get an entire \(2\)-category of monads inside \(C\)!

What is a morphism of monads? A monad functor \((X_1, S_1, \eta_1, \mu_1) \to (X_2, S_2, \eta_2, \mu_2)\) (i.e. a \(1\)-cell in the \(2\)-category of monads in \(C\)) is given by

• a \(1\)-cell \(u : X_1 \to X_2\)
• a \(2\)-cell \(\lambda : S_2 u \to u S_1\) (Note, this is not backwards! This is what we will need to map algebras of the firs monad to algebras of the second.)

satisfying the axioms:

• \(\eta_{S_2} u ; \lambda = u \eta_{S_1}\)
• \(S_2 \lambda ; \lambda S_1 ; u \mu_{S_1} = \mu_{S_2} ; \lambda\)

A monad transformation (i.e. a \(2\)-cell in the \(2\)-category of monads in \(C\)) is given by

• a \(2\)-cell \(\sigma : u_1 \to u_2\), satisfying \(\sigma S_2 ; \lambda_2 = \lambda_1 ; S_1 \sigma\) (something like that, see pasting diagrams of \(2\)-cells in the video).

Distributive laws 4

https://www.youtube.com/watch?v=FZeoHPRoBVk

Distributive laws, even more formally!

Consider the \(2\)-category of monads \(\mathbf{Mnd}(C)\) in an arbitrary \(2\)-category \(C\); monads in \(\mathbf{Mnd}(C)\) are distributive laws!

Recall that a monad in an arbitrary \(2\)-category is a \(0\)-cell equipped with an endo-\(1\)-cell and appropriate \(2\)-cells \(\eta\) and \(\mu\). In \(\mathbf{Mnd}(C)\):

• A \(0\)-cell in \(\mathbf{Mnd}(C)\), that is, a monad in \(C\) \((X,S)\).
• A \(1\)-cell \((X,S) \to (X,S)\), that is, a functor \(T : X \to X\) and \(\lambda : ST \to TS\).
• \(2\)-cells \(\eta\) and \(\mu\). Can check that these turn \(T\) into a monad.
• Axioms on \(\lambda\) give exactly what is needed to make it a distributive law.

Summarizing more concisely/informally, a monad in \(\mathbf{Mnd}(C)\) is

• A \(0\)-cell \(X\)
• A pair of monads \(S\),\(T\)
• A distributive law \(\lambda : ST \to TS\).

Consider the map \(C \mapsto \mathbf{Mnd}(C)\). This actually defines an endofunctor \(\mathbf{Mnd}(-)\) on \(2\)-\(\mathbf{Cat}\), the category of (strict) \(2\)-categories and (strict) \(2\)-functors. In fact, Street showed that \(\mathbf{Mnd}(-)\) is a monad! The “monad monad”.

The multiplication has type \(\mathbf{Mnd}(\mathbf{Mnd}(C)) \to \mathbf{Mnd}(C)\). Recall that objects in \(\mathbf{Mnd}(\mathbf{Mnd}(C))\) are a pair of monads \(S\),\(T\) plus a distributive law. In fact, the distributive law is precisely what is needed to make \(TS\) into a monad, which is the monad returned by the multiplication.

Group Objects and Hopf Algebras

Group Objects and Hopf Algebras 1

https://www.youtube.com/watch?v=p3kkm5dYH-w

Take the idea of a group and develop it categorically, first in the category of sets and then transport it into other categories (though it may not be completely obvious what properties of \(\mathbf{Set}\) we are using).

A group is of course a set \(G\) with an associative binary product, inverses, and an identity element. Let’s make this categorical: don’t want to talk about internal structure of \(G\) but just about \(G\) as an object in \(\mathbf{Set}\).

So a group is:

• an object \(G \in \mathbf{Set}\)
• a multiplication morphism \(\mu : G \times G \to G\)
• an inverse morphism \(\gamma : G \to G\)
• a unit morphism \(\eta : 1 \to G\) (i.e. “universal element”)

together with axioms expressed as commutative diagrams:

• \((id \times \mu) ; \mu = (\mu \times id) ; \mu\)
• \((\eta \times id) ; \mu = id = (id \times \eta) ; \mu\) (note to be pedantic we also need to use \(\lambda : G \to 1 \times G\) and \(\rho : G \to G \times 1\))
• \(\Delta ; (id \times \gamma) ; \mu = \varepsilon ; \eta\)

where \(\Delta : G \to G \times G\) is the diagonal map (note the fact that we are using \(\Delta\) is the most interesting part; see forthcoming lectures) and \(\varepsilon : G \to 1\) is the unique map to a terminal set.

Group Objects and Hopf Algebras 2

https://www.youtube.com/watch?v=kJ2X_U7X5WA

Note just \(\mu\) and \(\eta\) together with axioms (forgetting about \(\gamma\) and its axioms) is the definition of a monoidal category. Not surprising since a group is a monoid with inverses.

Recall \(\Delta : G \to G \times G\). We get that for free from the fact that the monoid we are using is really the categorical product; \(\Delta\) can be easily defined using the universal property of categorical product.

In fact, every set \(S\) is a comonoid in a unique way, since \(\times\) is a categorical product. That is, a comonoid on a set \(S\) is given by

• a comultiplication \(\Delta : S \to S \times S\)
• a counit \(\varepsilon : S \to 1\)
• satisfying coassociativity and counit axioms.

And note we used \(\Delta\) and \(\varepsilon\) in the definition of a group, in particular in the axioms for \(\gamma\).

Group Objects and Hopf Algebras 3

https://www.youtube.com/watch?v=wAeHrtKMTHM

The definition given last time won’t work in general for any monoidal category, but it does work for any Cartesian category (that is, monoidal categories where the monoidal operation is categorical product). Examples of Cartesian categories, in which it therefore makes sense to have group objects, include:

• \(\mathbf{Set}\)
• \(\mathbf{Top}\) (category of topological spaces, with Cartesian product toplogy)
• \(\mathbf{Diff}\) (cat. of smooth manifolds?)
• \(\mathbf{Grp}\) (groups)
• \(\mathbf{Cat}\) (categories)

Let’s see what a group object looks like in each of these examples.

• In \(\mathbf{Set}\), a group object is a group.
• In \(\mathbf{Top}\), a topological group.
• In \(\mathbf{Diff}\), a Lie group.
• In \(\mathbf{Grp}\), it turns out a group object is an Abelian group! (Details left as an exercise.)
• In \(\mathbf{Cat}\), we get a “crossed module”.

What about non-Cartesian monoidal categories? Simplest example is \(\mathbf{Vect}\), category of (finite-dimensional) vector spaces with linear maps. Monoidal structure given by tensor product and complex numbers. Tensor product defined by

\(V \otimes W = \{ \sum_t \alpha_t (v_t \otimes w_t) \mid v_t \in V, w\_t \in W \} / [(\alpha_1 v_1 + \alpha_2 v_2) \otimes w \sim \alpha_1 (v_1 \otimes w) + \alpha_2(v_2 \otimes w) \text{ and symmetrically}]\)

Suppose \(\{v_i\}\) is a basis for \(V\) and \(\{w_j\}\) is a basis for \(W\), then \(\{v_i \otimes w_j\}\) is a basis for \(V \otimes W\).

The point is that \(\mathrm{dim}(V \otimes W) = \mathrm{dim}(V) \times \mathrm{dim}(W)\), but that’s different than \(\mathrm{dim}(V \times W) = \mathrm{dim}(V) + \mathrm{dim}(W)\), so \(\mathbf{Vect}\) is not Cartesian.

Group Objects and Hopf Algebras 4

https://www.youtube.com/watch?v=zZn9ZETVkF8

We still want to be able to define group objects in monoidal categories which are not Cartesian.

Recall: if we have a monoidal category \((C, \times, 1)\) where \(\times\) is the categorical product, then every object \(X \in C\) is a comonoid \((X, \Delta, \varepsilon)\) in a unique way, and every morphism is a comonoid map.

Notation: in \(\mathbf{Set}\), an object with an associative binary operation and an identity is called a monoid; in \(\mathbf{Vec}\) it’s called an algebra. So when we generalize to arbitrary categories sometimes “monoid” is used, sometimes “algebra”.

A Hopf algebra is a group object in a general monoidal (tensor) category. Details next time.

Group Objects and Hopf Algebras 5

https://www.youtube.com/watch?v=gmxZ_KCRZho

A Hopf algebra \(H\) in a (braided) monoidal category is as follows. We don’t get comonoid stuff for free any more so we have to put it in “by hand”.

• comonoid \(\Delta : H \to H \otimes H\) and \(\varepsilon : H \to 1\)
• monoid \(\mu : H \otimes H \to H\) and \(\eta : 1 \to H\)
• “antipode” or inverse \(\gamma : H \to H\)

(See video for string diagrams.) Note the monoid and comonoid also need to be “compatible”: this is where the braidedness comes in. In particular \(\mu\) and \(\eta\) need to be comonoid morphisms. So we need \(H \otimes H\) to be a coalgebra.

Lemma: suppose \(H\), \(K\) are comonoids. Then \(H \otimes K\) is a coalgebra if the category is braided: \(H \otimes K \to (H \otimes H) \otimes (K \otimes K)\) using comonoid structures on \(H\) and \(K\), and then using (associativity and) braiding we can flip inner \(H \otimes K\) around to get \((H \otimes K) \otimes (H \otimes K)\).

Can then write down what it means for \(\mu\) to be a coalgebra map aka comonoid morphism; left as an exercise (or the next video).

Group Objects and Hopf Algebras 6

https://www.youtube.com/watch?v=Gv1sRLOwVWA

String diagram showing comonoid \(\Delta\) for \(H \otimes K\).

\(\mu\) and \(\eta\) should be a comonoid morphism, i.e. must commute with \(\Delta\) (string diagram) and also with \(\varepsilon\) (another string diagram).

There seems to be some asymmetry: monoid + comonoid + monoid must be comonoid morphisms. But it’s the same to say that the comonoid must be monoid morphisms.

Ends

Ends 1

http://youtu.be/mxI9ba6Rexc

Given a functor \(T : C^{op}\times C \to D\), an end \(\int_{c \in C} T(c,c)\) is an object in \(D\) which is “limit-like” in some sense.

Ends are not as common as coends (and perhaps not as intuitive?). Two particular places where ends do show up:

• natural transformations (especially in enriched setting; see Ends 2)
• reconstruction theorems (recover an algebra from category of its representations, i.e. Tannaka reconstruction, see Ends 3)

Definition:

• A wedge \(x \stackrel{\bullet}{\to} T\) consists of
  • an object \(x \in D\)
  • a family of \(D\)-morphisms \(\omega_c : x \to T(c,c)\) for all \(c \in C\)
  • such that for all \(f : c \to c'\) the obvious square with vertices \(x\), \(T(c,c)\), \(T(c',c')\), and \(T(c,c')\) commutes. (Dinaturality/extranaturality.)

  

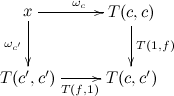
  • This is in some sense a generalization of a cone.

• An end is a universal wedge, i.e. a wedge \(E \stackrel{\bullet}{\to} T\) such that if \(x \stackrel{\bullet}{\to} T\) then there exists a unique morphism \(x \to E\) through which the components of \(x\) factor.

Note we write the object \(E\) using the intergral notation, \(\int_{c \in C} T(c,c)\) (the morphisms of the wedge are left implicit).

Ends 2

http://youtu.be/gyc86NFT0Sw

Simple example of an end: \(T = \mathrm{Hom} : C^{\text{op}} \times C \to \mathbf{Set}\). In this case a wedge \(x \stackrel{\bullet}{\to} T\) consists of:

• some \(x \in \mathbf{Set}\)
• for each \(c \in C\) a function \(\omega_c : x \to \mathrm{Hom}(c,c)\)
• such that \(\forall f : c \to c'\) we have \(\omega_c; f \circ - = \omega_{c'}; - \circ f\).

That is, for every \(n \in x\) we have \(\omega_c(n) = n_c : c \to c\), such that \(f \circ n_c = c_{c'} \circ f\). i.e. the family \(n_c\) are the components of a natural transformation \(Id_C \to Id_C\).

Note this goes in the other direction too, that is, a wedge \(x \stackrel{\bullet}{\to} \mathrm{Hom}\) is precisely the same thing as a function \(x \to \mathrm{Nat}(Id_C, Id_C)\). Therefore, the universal such \(x\) is precisely this set of natural transformations. (Can be thought of as “set of symmetries” of a category. Also the Hochschild cohomology.)

Ends 3

http://youtu.be/TfSUxhCNZZ0

More examples. First, straightforward generalization: given functors \(F, G : C \to E\), form the bifunctor \(\mathrm{Hom}_E(F(-), G(-)) : C^{op}\times C \to \mathbf{Set}\). Then we can see that

\(\int_{c \in C} \mathrm{Hom}_E(F(c),G(c)) = \mathrm{Nat}(F,G)\).

(Proof is just a small generalization of the proof in Ends 2, left as exercise.) Useful in an enriched context, can use this end to construct an object of natural transformations instead of a set.

Another example, “baby Tannaka reconstruction” (see Tannaka duality and reconstruction theorem on nlab).

• \(M\) is a monoid in the category of sets.
• \(M\)-\(\mathbf{Set}\) is the category of sets that \(M\) acts on
• \(U : M\text{-}\mathbf{Set} \to \mathbf{Set}\) is the forgetful functor.
• Result: \(\int_{(S,\sigma) \in M\text{-}\mathbf{Set}} \mathrm{Hom} (U(S,\sigma), U(S,\sigma)) \cong \mathrm{Nat}(U,U) \cong M\). (In general, natural transformations over forgetful functor reconstructs algebraic objects.)

Proof (application of Yoneda):

• Let \(\mu : M \times M \to M\) be monoid operation and \(e\) the identity.
• An \(M\)-set consists of a set \(S\) together with an action \(\sigma : M \times S \to S\). Morphisms \((S,\sigma) \to (R,\rho)\) are just functions \(S \to R\) which commute with the actions (“equivariant maps”).
• Note \(U\) is representable:
  • Consider the \(M\)-set \(M^l = (M, \mu)\) (“left-regular representation of \(M\)”)
  • Define \(\mathrm{Hom}(M^l, (S, \sigma)) \to S\) by \(f \mapsto f(e)\).
  • Note \(f(e)\) determines \(f\) since \(f\) is equivariant: \(f(m) = f(m \cdot e) = m \cdot f(e)\). In fact \(\mathrm{Hom}(M^l, (S, \sigma)) \cong S\).
  • Thus \(U = \mathrm{Hom}(M^l, -)\).
• So \(\mathrm{Nat}(U,U) = \mathrm{Nat}(\mathrm{Hom}(M^l,-), \mathrm{Hom}(M^l,-))\), and by (co-?)Yoneda, this is just \(\mathrm{Hom}(M^l, M^l) = U(M^l) = M\).

Ends 4

http://youtu.be/3hOtm0paWXY

Combine some of the previous examples. Recall

• \(\int_C \mathrm{Hom} \cong \mathrm{Nat}(Id,Id)\) (Ends 2)
• \(\int_{M\text{-}\mathbf{Set}} \mathrm{Hom}_{\mathbf{Set}}(U(-), U(-)) \cong M\) (Ends 3)

What happens if we combine these two results? First, look at the end from last time:

• Let \(\Phi \in \int_{M\text{-}\mathbf{Set}} \mathrm{Hom}_{M\text{-}\mathbf{Set}}(U -,U -) = \mathrm{Nat}(U,U)\) be a natural transformation on \(U\). That is, \(\Phi_{(R,\rho)}\) is a function \(R \to R\), such that \(\Phi\) commutes with the underlying function of any equivariant map, i.e.

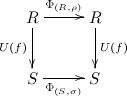
• As we showed last time, \(\Phi_{(R,\rho)} = \rho(m)\) for some \(m \in M\).
• Note \(\Phi_{(R,\rho)}\) is just a function \(R \to R\), but has to commute with equivariant functions.

Now look at the end of the bare hom-functor in the category of \(M\)-sets. i.e. \(\int_{M\text{-}\mathbf{Set}} \mathrm{Hom}_{M\text{-}\mathbf{Set}}(-,-) = ?\)

• Now if \(\Theta \in \int_{M\text{-}\mathbf{Set}} \mathrm{Hom}_{M\text{-}\mathbf{Set}}(-,-)\), we have

  

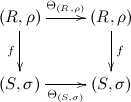
• What’s the difference? \(\Theta\) is now a family of equivariant maps. But note equivariant maps are determined by their underlying function. So any diagram of this form implies one of the previous form; the only thing we’ve added is that \(\Theta\) itself has to be equivariant (in the previous case \(\Phi\) could be any function). So in fact we have

  \(\int \mathrm{Hom}(-,-) \subseteq \int \mathrm{Hom}(U -, U -) = M\).

  i.e. we’re picking out some subset of \(M\). Question: which subset is it? That is, given such a \(\Theta_{(R,\rho)}\) we know \(\Theta_{(R,\rho)} = \rho(m)\) for some \(m\); which \(m\)’s can we get?

• Consider the left-regular representation \(M^l\) again. Then we know \(\Phi_{M^l} : M^l \to M_l\) is just left-multiplication by some \(m \in M\). But it has to commute with equivariant maps; picking the action on the particular element \(e\), this means for all \(n \in M\)

  \(n \cdot \Phi_{M^l}(e) = \Phi_{M^l}(n \cdot e)\)

  that is, \(nm = mn\), i.e. \(m \in Z(M)\).

• So we conclude \(\int_{M\text{-}\mathbf{Set}} \mathrm{Hom}_{M\text{-}\mathbf{Set}}(-,-) = Z(M)\).

Adjunctions from morphisms

Adjunctions from morphisms 1

https://www.youtube.com/watch?v=SzzHjpRmrLU

General phenomenon: associate some category \(C(X)\) to an object \(X\). For example:

• In representation theory, to a group or algebra we associate a category of modules or representations.
• In algebraic topology, to a space \(X\) we associate \(\mathbf{Vect}(X)\) (category of “bundles”?)
• In algebraic geometry, to an algebraic variety associate the category of sheaves.
• In logic, to a set of terms associate a category of subsets (predicates) over the terms.
• In analysis, to a metric space \(X\) associate a category of Lipschitz functions \(X \to \mathbb{R}\).

Question: if we have a morphism \(f : X \to Y\), how does that relate to the categories \(C(X)\) and \(C(Y)\) associated to \(X\) and \(Y\)?

We often get some sort of “pullback” functor \(f^* : C(X) \leftarrow C(Y)\). (Also often get some sort of monoidal structure on \(C(X)\) and \(C(Y)\), and \(f^*\) is often monoidal.)

We also get various “pushforwards” \(f_* : C(X) \to C(Y)\), right adjoint to \(f^*\). In some situation we also get a left adjoint to \(f^*\).

This is the beginning of the story of “Grothendieck’s 6 operations”. Lots of similar structure arises in all these different areas.

Adjunctions from morphisms 2

https://www.youtube.com/watch?v=jAQfNGEOass

Baby examples of some particular adjunctions (in generality, they show up in Grothendieck’s 6 operations, Frobenius reciprocity, …). Idea: start with (e.g.) sets; to each set associate a category; to each morphism between sets we will get functors between the categories.

• To the set \(X\) associate the slice category \(\mathbf{Set}/X\).
  • Think of the objects of this slice category, \(E \to X\), as “bundles over \(X\)”: a base space \(X\) and a set above that, where each element of \(X\) is associated to its fiber/preimage.
  • Another way to think of this is as a functor \(\hat{E} : X \to \mathbf{Set}\) (considering \(X\) as a discrete category), that picks out the fiber of each element of \(X\).

• There is actually an equivalence of categories \(\mathbf{Set}^X \cong \mathbf{Set}/X\).

• What about maps between sets? e.g. \(f : X \to Y\). As we’ll see, we get three associated maps \(f^* : \mathbf{Set}^Y \to \mathbf{Set}^X\), \(f_* : \mathbf{Set}^X \to \mathbf{Set}^Y\), and \(f_! : \mathbf{Set}^X \to \mathbf{Set}^Y\), with \(f_! \dashv f^* \dashv f_*\). Details in the next lecture.

Adjunctions from morphisms 3

https://www.youtube.com/watch?v=tWhB7E-HS8Y

• Given \(f : X \to Y\), define the “pullback” of a bundle over \(Y\) to a bundle over \(X\) written \(f^* : \mathbf{Set}^Y \to \mathbf{Set}^X\): to each \(x \in X\) we associate the fiber of \(f(x) \in Y\). That is,

  \(f^* \hat{F} = \hat{F} \circ f.\)

• Now for the other direction. Idea: given a bundle over \(X\) and \(f : X \to Y\), for each \(y \in Y\) we have a set \(f^{-1}(y) \subseteq X\) which are sent to that \(y\) by \(f\); we have to somehow combine their fibers to yield a fiber for \(y\). Several ways we could imagine doing it: disjoint union, product? In this case we want the product. That is,

  \(\displaystyle (f_* \hat{E})(y) = \prod_{x \in f^{-1}(y)} \hat{E}(x).\)

(Foreshadowing: taking the disjoint union gives us another adjoint.)

Adjunctions from morphisms 4

http://youtu.be/Cf7hCiTspJc

Proof of the adjunction \(f^* \dashv f_*\). (Come up with your own mnemonic to remember which way around the adjunction goes; suggested: think of a “falling star”.)

• Notation: \(\mathrm{Hom}_X(a,b)\) instead of \(\mathbf{Set}^X(a,b)\) or \(\mathrm{Hom}_{\mathbf{Set}^X}(a,b)\)

• Such hom-sets are a collection of maps between fibers, one for each base point.

• So we have \(\mathrm{Hom}_X(f^* \hat F, \hat E) = \prod_{x \in X} \mathrm{Hom}(f^* \hat F (x), \hat E (x)) = \prod_{x \in X} \mathrm{Hom}(\hat F (f(x)), \hat E (x))\).

• We can partition \(X\) as preimages of elements of \(Y\) under \(f\). So the above is equal to \(\prod_{y \in Y} \prod_{x \in f^{-1}(y)} \mathrm{Hom}(\hat F (y), \hat E (x))\).

• A product of hom-sets is isomorphic to a hom-set into a product (i.e. \(A^X B^X = (AB)^X\)), so this is equal to \(\prod_{y \in Y} \mathrm{Hom}(\hat F (y), \prod_{x \in f^{-1}(y)} \hat E (x))\).

• By definition of \(f_*\), this is \(\prod_{y \in Y} \mathrm{Hom}(\hat F (y), (f_* \hat E) (y))\).

• Finally, by definition of \(\mathrm{Hom}_Y\), this is \(\mathrm{Hom}_Y (\hat F, f_* \hat E)\).

• Of course technically we would need to show naturality as well, but this is the basic idea.

Adjunctions from morphisms 5

https://www.youtube.com/watch?v=MSOGEtW39qM

Last time, we proved an adjunction \(f^* \dashv f_*\), i.e.

\(\mathrm{Hom}_X (f^* \hat F, \hat E) \cong \mathrm{Hom}_Y (\hat F, f_* \hat E).\)

In fact, we showed that both are isomorphic to

\(\prod_{x \in X} \mathrm{Hom}(\hat F (f(x)), \hat E(x)).\)

i.e. given some \(f : X \to Y\), for each \(x\) we get a map going the other way, from the fiber over \(f(x)\) to the fiber over \(x\). (See the video for a nice picture.) But we can imagine turning these maps around, giving

\(\prod_{x \in X} \mathrm{Hom}(\hat E(x), \hat F(f(x))).\)

Using the same trick as last time, this is equivalent to \(\prod_{y \in Y} \prod_{x \in f^{-1}(y)} \mathrm{Hom} (\hat E (x), \hat F (y))\), which is in turn equivalent to

\(\prod_{y \in Y} \mathrm{Hom} (\coprod_{x \in f^{-1}(y)} \hat E (x), \hat F (y))\)

(since \(\mathrm{Hom}(-,B)\) turns limits into colimits; concretely, note that \(A^X A^Y = A^{X + Y}\)).

This gives us a left adjoint \(f_! \dashv f^*\), defined by

\(\displaystyle (f_! \hat E)(y) = \coprod_{x \in f^{-1}(y)} \hat E(x).\)

Remark: note that if we view bundles over \(X\) as objects of the slice category \(\mathbf{Set}/X\), \(f_!\) is just composition.

Double Categories

Double Categories

https://www.youtube.com/watch?v=kiCZiSA2W3Q

Internal categories in \(\mathbf{Cat}\). Recall that an internal category in \(E\) is a pair of objects \(A\) (representing objects) and \(B\) (representing morphisms), and a pair of parallel arrows \(s,t : B \to A\) in \(E\) recording the source and target of each morphism, all suitably equipped with unit and composition.

If \(A\) and \(B\) are themselves categories, and \(s\) and \(t\) are functors, then \(B\) itself has sets of objects \(B_0\) and morphisms \(B_1\) with source and target functions, and the same for \(A\). Then the functors \(s\) and \(t\) have actions on morphisms and objects, so we get a square with two parallel arrows on each side.

• \(A_0\) are \(0\)-cells.
• \(A_1\) are “vertical \(1\)-cells”.
• \(B_0\) are “horizontal \(1\)-cells”.
• \(B_1\) are \(2\)-cells, which sit inside squares (not inside the area between two parallel \(1\)-cells): each element of \(B_1\) has corresponding sources and targets in both \(B_0\) and \(A_1\), and the double commuting square described above ensures that the sources and targets of those have to match up in a square.

What about composition? Note \(B\) and \(A\) already come equipped with composition, which together give us “vertical composition” of \(2\)-cells. Composition in the internal category gives horizontal composition of \(2\)-cells.

Note if all vertical \(1\)-cells are identities, this collapses to the usual idea of a \(2\)-category. (Or symmetrically, with horizontal \(1\)-cells being identities.)

Spans

Spans 1

https://www.youtube.com/watch?v=SQfUXOCMUhI

NOTE: There seems to be no catsters video actually explaining what a “bicategory” is. According to the nlab it is a weaker version of a 2-category, where certain things are required to hold only up to coherent isomorphism rather than on the nose.

Let \(E\) be a category with (chosen) pullbacks. \(\mathbf{Span}(E)\) is a bicategory with

• \(0\)-cells the objects of \(E\)
• \(1\)-cells \(A \to B\) are spans \(A \leftarrow S \rightarrow B\).

• \(2\)-cells are morphisms between \(1\)-cells, that is, spans. So a \(2\)-cell between \(A \leftarrow S \rightarrow B\) and \(A \leftarrow S' \rightarrow B\) is a morphism \(S \to S'\) which makes things commute.

• \(1\)-cell composition: use pullback. Is this associative? Yes, up to isomorphism (because of universal property of pullbacks) but not on the nose. (Hence we get a bicategory and not a strict \(2\)-category.)

• Vertical \(2\)-cell composition: just composition of the underlying morphisms.

• Horizontal \(2\)-cell composition: the two pullbacks induce a morphism between them.

Can check all the axioms etc.

Now, note monads can be constructed inside any bicategory, and are given by

• a \(0\)-cell \(X\)
• a \(1\)-cell \(T : X \to X\)
• \(2\)-cells \(\eta\) and \(\mu\) satisfying the usual monad axioms (slightly modified to make them make sense)

It turns out that monads in \(\mathbf{Span}(E)\) are great! For example, monads in \(\mathbf{Span}(\mathbf{Set})\) are small categories. Next time we’ll see why.

Spans 2

https://www.youtube.com/watch?v=Jn5dZuebeXU

Monads in \(\mathbf{Span}(Set)\) are small categories. These notes make a lot more sense when you can look at the diagrams. Watch the video or work out the diagrams yourself.

We have

• a \(0\)-cell, i.e. a set \(C_0\).
• a \(1\)-cell from \(C_0\) to itself, i.e. a span \(C_0 \stackrel{s}{\leftarrow} C_1 \stackrel{t}{\rightarrow} C_0\) (idea is that \(C_1\) will be the set of morphisms, and \(s\) and \(t\) will pick out the source and target objects)
• a \(2\)-cell \(\eta\) from \(1\) (the boring span with all the same object and identity morphisms) to the \(1\)-cell given above. This ends up being a function \(f : C_0 \to C_1\) such that \(f ; s = f ; t = id\), that is, \(f\) takes each object in \(C_0\) to a morphism in \(C_1\) having that object as both its source and target.
• a \(2\)-cell \(\mu : C_1^2 \to C_1\). \(C_1^2\) is given by a pullback: a pair of morphisms such that the target of the first equals the source of the second, i.e. a composable pair. \(\mu\) therefore has to take a composable pair and produce a single morphism in \(C_1\) such that its source equals the source of the first and its target equals the target of the second.

And of course there are some monad laws which amount to the category laws.

More generally, monads in \(\mathbf{Span}(E)\) are categories internal to \(E\). I.e.

• an “objects object” \(C_0\)
• a “morphisms object” \(C_1\)
• source and target maps \(C_1 \to C_0\)
• identities and composition as before.

Multicategories

Multicategories 1

http://www.youtube.com/watch?v=D_pPNgGZYDs

Like categories, but morphisms have multiple objects as their source.

A (small) multicategory \(C\) is given by

• a set of objects, \(\mathrm{ob} C\)
• For all \(x_1, \dots, x_n, x\), a set \(C(x_1, \dots, x_n, x)\) of morphisms.
• Composition: a morphism with \(n\) inputs can be composed with \(n\) morphisms, producing a result which is a morphism with the concatenation of inputs of all the \(n\) morphisms.
• Identity morphisms, with just one input and output.

Note that one can have a morphism with no inputs.

This can all be expressed nicely using the “free monoid monad” (i.e. list monad). Let \(T\) be the free monoid monad on \(\mathbf{Set}\), i.e. the list monad; that is, \(T\) sends each set \(S\) to the free monoid on \(S\) (i.e. lists of \(S\)).

Make a bicategory of \(T\)-spans. Just as monads in the category of spans were small categories, monads in the (bi)category of \(T\)-spans are multicategories.

\(T\)-span has:

• \(0\)-cells are sets
• \(1\)-cells are spans \(T A \leftarrow S \to B\).
• \(2\)-cells are just span morphisms.
• Composition uses pullbacks and multiplication of \(T\).
• Identity is \(T\)-span \(T A \leftarrow A \to A\) using \(\eta\) and \(id\).

Bicategory axioms follow from monad laws for \(T\). Next time: monads in this category are multicategories.

Multicategories 2

https://www.youtube.com/watch?v=WytjdlserwU

We’ve seen that monads in Span are categories.

We’ve seen a category of \(T\)-spans, spans with a \(T\) on the left. We’ll see that monads in \(T\)-\(\mathbf{Span}\) are multicategories.

Recall that \(T\) is the list monad.

A monad in \(T\)-\(\mathbf{Span}\) is:

• a set \(C_0\) (which will represent objects of the multicategory)
• a \(1\)-cell \(C_0 \to C_0\) is a \(T\)-span, i.e. an object \(C_1\) (representing morphisms of the multicategory) together with morphisms from \(C_1\) to \(T\ C_0\) (picking out the sequence of input objects) and from \(C_1\) to \(C_0\) (picking the target object).
• a \(2\)-cell \(\eta\), representing the identity morphism with a single input (see video for a commutative diagrma)
• a \(2\)-cell \(\mu\) which represents composition in a multicategory. See video for diagram!

Key point: we can actually do this with other monads \(T\)! And even on other categories with pullbacks, as long as \(T\) preserves pullbacks (and \(\eta\) and \(\mu\) commutative diagrams are pullbacks). This yields a notion of a \(T\)-multicategory. The source of each morphism is not just a list of objects but a \(T\)-structure of objects.

Metric Spaces and Enriched Categories

Metric Spaces and Enriched Categories 1

https://www.youtube.com/watch?v=be7rx29eMr4

Idea due to Lawvere. A metric \(d\) on a metric space satisfies:

• Triangle inequality: \(d(a,b) + d(b,c) \geq d(a,c)\)
• \(0 \geq d(a,a)\)

Compare to the data for a category, written in a slightly funny way:

• \(\mathrm{Hom}(a,b) \times \mathrm{Hom}(b,c) \to \mathrm{Hom}(a,c)\)
• \(\{\star\} \to \mathrm{Hom}(a,a)\)

These look remarkably similar! In fact, they are both examples of enriched category. We’ll start with a normal category and show how to generalize it to an enriched category.

Let \(C\) be a category. We have:

• a collection \(\mathrm{Ob}(C)\)
• \(\forall a,b \in \mathrm{Ob}(C)\), \(\mathrm{Hom}(a,b) \in \mathrm{Ob}(\mathbf{Set})\)
• \(\forall a,b,c \in \mathrm{Ob}(C)\), \(\exists \mathrm{Hom}(a,b) \times \mathrm{Hom}(b,c) \to \mathrm{Hom}(a,c)\)
• \(\forall a \in \mathrm{Ob}(C)\), \(\exists \{\star\} \to \mathrm{Hom}(a,a)\)
• …satisfying associativity and unit laws.

Important thing to note: composition and identity are morphisms in \(\mathbf{Set}\). What properties of \(\mathbf{Set}\) have we used? Just a Cartesian product and the one-element set \(\{\star\}\). Right generalization is a monoidal category.

In particular, if \((V, \otimes, I)\) is a monoidal category, we can define categories enriched in \(V\). Definition becomes:

\(C\) is a \(V\)-category (category enriched in \(V\)):

• collection \(\mathrm{Ob}(C)\) as before
• \(\mathrm{Hom}(a,b) \in \mathrm{Ob}(V)\), i.e we don’t have hom-sets but hom-objects that live in the category \(V\)
• The composition map is a morphism \(\mathrm{Hom}(a,b) \otimes \mathrm{Hom}(b,c) \to \mathrm{Hom}(a,c)\) in \(V\)
• Identity morphisms are now given by a morphism \(I \to \mathrm{Hom}(a,a)\) in \(V\).
• …satisfying associativity and unit laws.

e.g. pick \(V\) to be category of Abelian groups (yields “additive category”), or category of vector spaces (yields “linear categories”).

What if we take \(V\) to be a non-concrete category? e.g. take the poset of nonnegative real numbers under \(\geq\). Can make this monoidal by taking the usual \(+\), identity is \(0\). Then it turns out that categories enriched in this poset category are metric spaces!

Metric Spaces and Enriched Categories 2

https://www.youtube.com/watch?v=0p3iS3Nf-fs

Explains in more detail how categories enriched in \((\mathbb{R}^+, \geq)\) poset (with monoidal structure given by \(+\) and \(0\)) are metric spaces.

• For each pair of objects we have a “Hom-object” which is a nonnegative real number. (“distance”)
• Composition is supposed to be a morphism \(\mathrm{Hom}(a,b) \otimes \mathrm{Hom}(b,c) \to \mathrm{Hom}(a,c)\). But \(\otimes\) is \(+\) and \(\to\) is \(\geq\), so this is the triangle inequality.
• Identity morphisms are given by \(I \to \mathrm{Hom}(a,a)\); in this context that says \(0 \geq \mathrm{Hom}(a,a)\), i.e. distance from \(a\) to itself is \(0\).
• Associativity and unit laws are vacuous.

This is actually a generalized metric space. More general than a metric space in several ways:

• Distance is not symmetric: \(d(a,b) \neq d(b,a)\). This actually has many real-world models (e.g. time to go between towns in the Alps).
• We might have \(d(a,b) = 0\) for \(a \neq b\).
• We allow “infinite” distances (???)

Now we can study metric spaces categorically.

Given two \(V\)-categories, a \(V\)-functor \(\Phi : C \to D\) consists of

• a map \(\mathrm{Ob}(C) \to \mathrm{Ob}(D)\), and
• for all \(a,b,c \in C\), \(\Phi : \mathrm{Hom}(a,b) \to \mathrm{Hom(\Phi a, \Phi b)}\) (a morphism in \(D\)) which has to commute with composition in the appropriate way.

In the generalized metric setting, such a \(\Phi\) is a nonexpansive map.

Metric Spaces and Enriched Categories 3

https://www.youtube.com/watch?v=kMSt_Ci54BE

Enriched natural transformations. There are actually various ways to generalize. Today: simple-minded version. Apparently if we generalize the notion of a set of natural transformations we get a slightly better definition—this will be covered in future videos. [editor’s note: to my knowledge no such future videos exist.]

Standard definition of a natural transformation \(\theta : F \to G\) given functors \(F,G : C \to D\). Problem: we are supposed to have \(\theta_x \in \mathrm{Hom}(F x, G x)\), but in the enriched setting \(\mathrm{Hom}(F x, G x)\) may not be a set, but just some object. So what should it mean for \(\theta_x\) to be an “element” of it?

Simple way around this: let \((V, \otimes, 1)\) be a monoidal category. We can define a canonical functor \(\Gamma : V \to \mathrm{Set}\) (“generalized elements”) which takes an object \(v \in V\) to the Hom-set \(\mathrm{Hom}(1,v)\).

e.g. if \(V = \mathrm{Set}\), \(\Gamma\) is the identity. Another example I don’t understand involving category of complex vector spaces.

In the example we care about, \(V = \mathbb{R}^+\), and \(I = 0\). In this case \(\Gamma\) sends \(v\) to the Hom-set \(0 \geq v\), that is, \(\{\star\}\) if \(v = 0\) and the empty set otherwise.

So now we can say that \(\theta_x\) should be a generalized element of \(\mathrm{Hom}(F x, G x)\).

So, let \(F, G\) be \(V\)-functors. Define a \(V\)-natural transformation \(\theta : F \to G\) as

• for all \(x \in C\), \(\theta_x \in \Gamma(\mathrm{Hom}(F x, G x))\).
• Big commuting diagram expressing naturality in the enriched setting (see the video).